Preface

The limits of my language mean the limits of my world.

- Ludwig Wittgenstein, Austrian Philosopher

The fields of audio engineering and music technology have wide-ranging applications in our lives. People are creating music, videos, livestreams, and more at a pace unlike ever before. And this trend is only accelerating with the advent of AI and machine learning. We now have speech-to-text, text-to-speech, automatic music transcription, automatic music creation, voice quality enhancement, and so much more at our fingertips. Hearing is one of the major ways in which we sense the world around us, and we are so fortunate to experience this digital revolution.

However, most people do not have the language to describe what they hear. A perfect example of this is the famous presentation by Leonard Bernstein at Harvard university. In the video, he uses several phrases that sound profound, but have no real substance.

• "The built-in, pre-ordained, universal, known as the harmonic series"

• "Dark, rich bass note"

• "Comparative richness of this low C"

• "Fundamental laws of physics"

• "The very nucleus and the cornerstone of most of the music we hear"

• "The foundation of western tonal music"

What exactly does it mean for a note to be "dark" and "rich"? What does it mean for something to be the "nucleus" of music? And if what he says is true, why can digitally-produced music escape the constraints of the "built-in, pre-ordained, universal" harmonic series? Obviously, Bernstein has the full knowledge and capability to explain and produce amazing music. The issue is that he avoids scary technical words like "integer" and "exponent" since they would be too confusing to his Harvard audience.

I'm not trying to needlessly dunk on fun and lighthearted educational content that was designed for a TV broadcast. In fact, Bernstein gives one of the the clearest and most concise presentations of harmonics that I've ever seen. His masterful distillation of the information sets him apart from the poor presentations seen in other media. The thing that those other presentation have in common with Bernstein's presentation is that the information about harmonics is is wrong, and we're going to find out why.

How Harmonics Actually Work

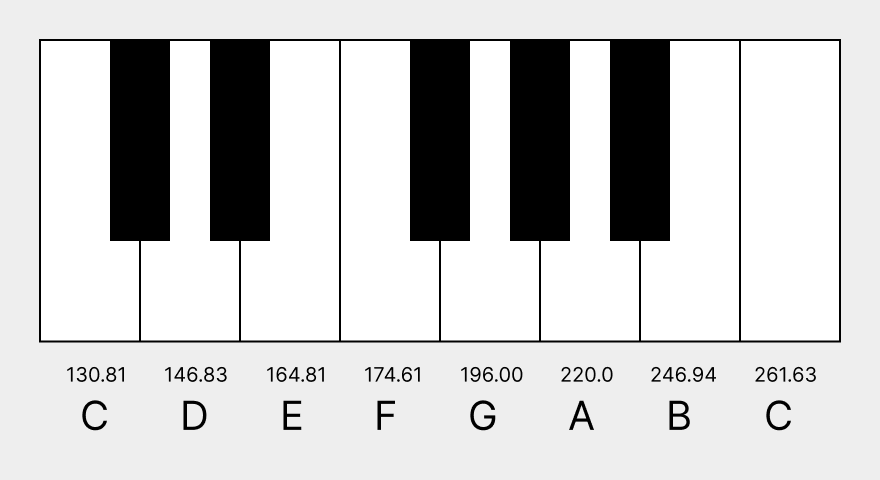
When a key on a piano is pressed, a hammer strikes a metal string that vibrates at a particular frequency. Each key has its own string, and each string vibrates at a different frequency. The note named C3 has a frequency of $130.81$ Hertz, or cycles per second.

As you travel up the piano, the frequencies increase exponentially. Every time you jump up one octave, for example from C3 to C4, the frequency doubles. This means that the frequency for C4 is $130.81 * 2 = 261.62$. This can be seen in Module 1.

Module 1

Image

Piano notes with their associated frequencies.

Where do those in-between frequencies come from? There are 12 half-steps or semitones between C3 and C4. You can count them yourself, making sure to include both the white keys and the black keys. Each half-step increase will multiply the frequency by $2^{1/12}$. For example, D3 has a frequency of $130.81 * 2^{2/12} = 146.83$, since D3 is two half-steps above C3.

As Bernstein points out, when C3 is pressed, there is not one frequency, but many frequencies that occur due to sympathetic resonance between the piano strings. He also flashes a picture similar to Module 2 on the screen.

Module 2

Image

An illustration of harmonics for piano strings.

The harmonics or overtones are integer multiples of the note that is being played. If C3 is pressed, then the following frequencies are produced.

$$\begin{aligned} 130.81 \text{ Hz} * 1 &= 130.81 \text{ Hz} & \text{\small First harmonic} \\ 130.81 \text{ Hz} * 2 &= 261.62 \text{ Hz} & \text{\small Second harmonic} \\ 130.81 \text{ Hz} * 3 &= 392.43 \text{ Hz} & \text{\small Third harmonic} \\ 130.81 \text{ Hz} * 4 &= 523.24 \text{ Hz} & \text{\small Fourth harmonic} \\ 130.81 \text{ Hz} * 5 &= 654.05 \text{ Hz} & \text{\small Fifth harmonic} \\ \end{aligned}$$

On the piano, these harmonics are the sequence of notes C3, C4, G4, C5, and E5. When the major triad of C, E, and G are played together, they not only sound beautiful but are mathematically beautiful as well. Because the harmonics are integer multiples of the fundamental frequency, the C, E, and G notes form nice frequency ratios with each other. For example, within the same octave, the frequency for G divided by the frequency for C is 3/2. For E and C the ratiuo is 5/4. Music has hidden mathematical structure that explains why we have an intrinsic love for music...

...except that's all wrong. If we look back at Module 1 and divide the frequencies, the ratio for E to C is $164.81 / 130.81 = 1.26$, which isn't quite $5/12$. Earlier in this preface, we saw that $2^{1/12}$ is the frequency multiplier when going up or down by one semitone. Theoretically, the is actually $2^{5/12} = 1.25992$, since there are five semitones going up from C to E.

What Happened Here

The word "octave" is the most egregious misnomer in world history. There are three ways to interpret the concept, none of which have anything to do with the number eight.

• When traversing up the piano looking only at the white keys, we would say that every seventh note is a C. In fact, we only use seven letters to name the white keys on a piano.

• When jumping from a note to the same-lettered note one octave higher, the frequency of the higher note is two times the frequency of the lower note.

• When calculating the frequencies using the standard reference frequency of 440 Hz for A4, we multiply or divide the reference frequency by some multiple $2^{1/12}$, sincere there are twelve semitones per octave.

The language we use often prevents us from effectively communicating abstract concepts. The fields of audio engineering and music technology are unfortunately some of the most susceptible to this issue since almost everyone has interest in music in one form or another. Children learning music are taught this incorrect information to the point that it becomes entrenched in all forms of media.

Who Cares?

You might be asking yourself, who cares that $1.25992$ is not equal to $1.25$ exactly. It's basically a rounding error, less than $1\%$ off from the theoretical value. To our ears, the CEG chord still sounds nice and harmonious. What's the problem then?

The world is not mathematically beautiful. It's extraordinarly messy, and if you want to get things done with audio, you can't rely on hand-wavy explanations from Redditors or gaudy tutorials with antique audio eqiupment from MIT. You need to be able to understand every step of the process, Otherwise, you are destined to poke and prod at thousands of knobs in your digital audio workstation and still fail to achieve the result you want.

Consider all the lossy steps that audio takes on its journey from a podcast host to your ears.

• Microphones record their own electrical noise.

• Microphones have a limited sample rate that limits what frequencies they can record.

• Digital signal processing inside the microphone itself can cause clipping or modify the audio trying to avoid clipping.

• Sampled audio is stored with limited-precision integers when written into a buffer.

• Audio is run through lossy compression algorithm from WAV to MP3.

• If your podcasting app equalizes volume levels across different podcast episodes, it runs dynamic range compression on the audio.

• If you are listening to the podcast at 2x speed, then a WSOLA or PSOLA algorithm is applied, which introduces artifacts. (This is why constant-frequency sounds have vibrato at 2x speed.)

• In order for your speakers to apply equalization to the audio, it needs to decompose the audio from samples into its constituent frequencies, which is imperfect because of spectral leakage.

• And finally, if you are wearing headphones with active noise cancellation, there is some noise that is added as a result of the digital signal processing. (For example, if you are in a nearly perfectly silent room with the Bose QC 45 headphones, you can hear a hissing sound when active noise cancellation is enabled.)

If you made it all the way to the end of this essay, you must be the kind of person who cares deeply about getting the details right. Hopefully you have that same passion for solving real-world problems. The incredible effectivness of machine learning and AI has caused an explosion of audio-related research that collectively adds billions of dollars of value to people's lives. If you would like to understand in-depth all of the audio-related research that is happening right now, check out Audio Internals: Digital Signal Processing for Software Applications.